緩和曲線

HOレイアウトの中間駅前後の750Rの曲線に緩和曲線を加えてレイアウトスペース見積もりの精度向上と思い、ここで緩和曲線。緩和曲線は、小学生のころ師の石田啓二先生よりお借りした(注1)TMS1968年11月号「長編成用のレイアウト」に再掲の、高級モデルノートからのR=914、Φ=15°のものをずっと参考にしていました。今回ネットで調べてみると、三次曲線の緩和曲線は、Φ=24.1°で曲線半径が極小かつほぼ一定になるという説明があって、とても参考になったので、自分でも少し考えてみることにしました。
今までも、レイアウトは、やや短めの緩和曲線でも、無いよりは良いだろうと考えていたので、鉄道文献の緩和曲線敷設方法で、先ず緩和曲線の長さＬを決めて計算するものも見つけて考えていたのですが、Ｌの振り分けが1:1になっている点など高級モデルノートの形状と違うので、やや混乱していました。sin ≒ tanの近似で誤差があるようで、当時の現場での作業を考慮したのだろうと思います。また、実際の鉄道では曲線カント前後の軌道ねじれによる脱線を重視しているようなのですが、模型での効果と考え方が違うと感じました。
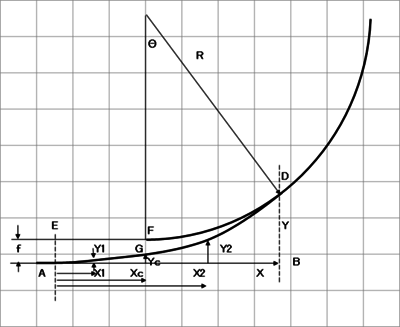
RとΦから緩和曲線を求めてみようと思います。(おきらく研究室の緩和曲線の作り方)が正確かつ分かりやすいので式を使わせていただきます。
曲線 y = a * x^3
曲率は κ = 6 * sqrt(a^2 * x^2 / ( 1 + 9 * a^2 * x^4 )^3 )
円曲線との接続がΦ(rad)の時のXを求めると、
曲線の傾き dy/dx = 3 * a * x^2
tan(Φ) = 3 * a * X^2
X = sqrt(tan(Φ) / (3 * a) )
Xでの曲率は、
κ = 6 * sqrt(a^2 * (tan(Φ) / (3 * a)) / ( 1 + 9 * a^2 * (tan(Φ) / (3 * a))^2 )^3)
aを求める、
κ = 6 * sqrt( a * (tan(Φ) / 3 ) / ( 1 + tan(Φ)^2 )^3 )
両辺二乗して、
κ^2 = 6^2 * ( a * (tan(Φ) / 3 ) / ( 1 + tan(Φ)^2 )^3 )
6^2で割ると、
κ^2 / 36 = a * (tan(Φ) / 3 ) / ( 1 + tan(Φ)^2 )^3
a = κ^2 * ( 1 + tan(Φ)^2 )^3 / (12 * tan(Φ) )

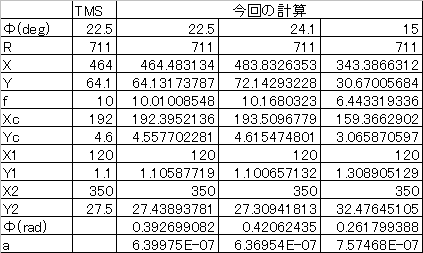
これでΦとＲから曲線の式が求まりますので、とりあえず精度など気にしないでエクセルで求めてみます。TMSの高級モデルノートの値とほぼ同じになるので、妥当な結果だと思います。任意のΦでの値が計算できますので便利かなと思います。もっとも模型の緩和曲線は見栄え重視なので、そんなに正確である必要が無いのは、皆さんのページに賛同します。でも趣味なので一応正確な値も欲しいかなということです。 (2017.3.5)
計算結果

参考までに、ΦとＲを入力して曲線を求める計算のExcelです

(注1) ずっとそう思っていましたが年号が小学生時代と合わないのに気がつきました。中学校の模型部で借りた本のようです。

	緩和曲線の長さLは、1/80スケールでだいたい400mm超えくらいが多いようで、1両半くらいですね。1両分くらいでも良いんじゃないのとケチケチ根性が出てきたので、手持ちのレールで様子を見てみることに。750R、Φ=15°の緩和曲線は、L=362mmです。充分な長さの感じです。750Rだと円曲線で連結面の曲がり方が大きくやや不自然かな。914Rは、緩和曲線が無いと直線からの入口での連結面のずれが大きいです。円曲線で連結面の曲がり方はまあガマンできる感じですね。なおフレキシブルレールは、750Rはコルク道床下にベニヤ板、914Rはベニヤ板道床です。はるか昔、学生時代に作ったものです。車両は、屋根が明るい色のは引越しでカプラーやボルスターが壊れてしまっていて、走行可能なのは客車しかなかったので黒です、一応切り妻のを使いました。 (2017.3.8)

レイアウトプランを具体化していくと914Rの緩和曲線が長いのが気になり、一部でΦ=8°の緩和曲線を考えていたので、確認してみました。#6ポイントのコルク道床が適当なのでフレキシブルレールを仮設してみました。お手軽なので精度はいい加減です。Φ=8°だと長さL=249.5mmです。レールを眺めた感じは良いですね。連結部分のくい違いの写真は、カーブ通過中に一番大きくなったところです。意外に大きいので、少し長くΦ=10°も比較してみました。円曲線のレール1本が30°なので整数分の一の10°の方が切り貼りし易いという理由もあります。あんまり変わらないですね、どちらも緩和曲線の円曲線側でくい違いが大きいようです。少し曲線の形を手で変えてみると良くなります。もともと3次曲線は曲率を滑らかに変化させる簡単な関数として使っているだけで、連結面のくい違いが最適になる関数というわけではないですね。くい違いが大きくなる曲率の小さい円曲線側での曲率の変化が少ない関数の方が好ましいのだろうと思います。お手軽工作なので、細かい事はなんとも言えませんが。ここまで分かれば、先ず3次曲線で仮に作っておいて、現物でくい違いを確認しながら小修正するのが現実的なようです。だったら30°の1/4のΦ=7.5°でどうだろうと、ケチケチ根性で実験。Φ=7.5°だとL=234.5mm、工作精度が悪いからだろうと思うのですが、くい違いはΦ=10°より良さそうに理屈とは逆に見えます。小修正してこれくらいにできれば良いように思います。(2017.10.19)

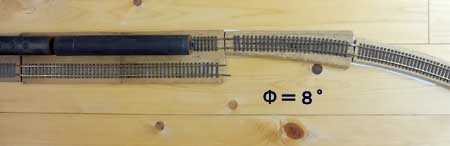
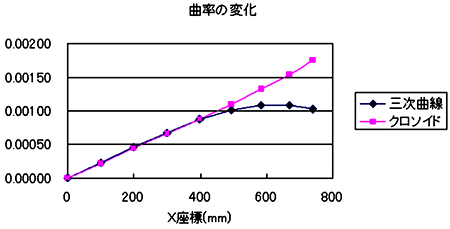いろいろ曲線を変えて確認してみたのですが、緩和曲線の長さが車両一両分程度では、連結部のくい違いに不満が残りそうです。緩和曲線に乗っている台車が2個だけでは効果が少ないのかもしれません。914Rで線路を眺めた感じは8°でも充分ですが、くい違いに関しては10°でも足りないようです。やはりTMSの「長編成用のレイアウト」の15°は、よく検討されています。1.5両分の長さの375mm(12.5°)以上で計画するのが良さそうです。先日の確認の写真を見ると、緩和曲線の長さが長くなる、7.5°→8°→10°の順に、連結部のくい違いの大きい場所が、直線寄りに移動しているのに気がつきました。さらに12°くらいになれば殆ど直線の部分に移動して、くい違いがとても少なくなるのだろうと思います。
鉄道では、敷設が容易という理由もあって三次曲線の緩和曲線が良く使われていて、曲率の変化が直線のクロソイド曲線を近似できているからという説明があったので、参考で曲率の変化を比較してみました。グラフの横軸は直線側からのX方向の長さです。クロソイド曲線は曲線の長さと曲率が比例するので、クロソイド曲線の線長100mm毎に、弦長を求め、このX座標を計算しました。あさかぜネットのWeb測量計算クロソイド曲線(弦角、弦長計算)を使わせていただきました。クロソイドパラメータA=600としました、弦角や弦長が良い感じになるように見当で決めたものです。このX座標での三次曲線の曲率を計算し比較しました。クロソイド曲線の曲率は線長に比例なので、比較しやすいように400mmで三次曲線と同じ数値になるように線長を換算(正規化)してあります。X=600mmの辺りが三次曲線での24°です。400mmあたりまでは近似と言えそうで、16°くらいです。16°～24°は、近似しなくなりますが、三次曲線は滑らかに曲率が変化して円曲線につながるのでこれはこれで良い緩和曲線と考えられます。滑らかな分、緩和曲線は長くなるのだろうと思います。16°以上は当鉄道には無縁なようですので、計算し易い三次曲線を基本で良いかな。(2017.10.24)

| TOPページ | TOP |